技術情報TECHNOLOGY

設計資料

本文中で使用する記号本文中で使用する記号を以下に示す。

φ: たわみ角　Deflection angle

M: トルク　Torque

l: ばね有効長さ　Spring length

I: 断面2次モーメント　
Moment of inertia

E: ヤング率　Young’s modulus

b: 板幅　Spring width

t: 板厚　Spring thickness

k: ばね定数　Spring constant

σ: 応力　Stress

Mv: 振動体の質量　Mass

χ: 振動体の回転半径　Radius

T: 振動体の周期　Period

N: 回転数　
Number of revolutions

d₁: シャフト径　Shaft radius

D₂: ケース径　Case radius

R_n: 自然半径　Natural radius

R₁: 従動軸半径　
Driven shaft radius

R₂: 駆動軸半径　
Drive shaft radius

P: 力　Force

1非接触形渦巻ばね

i. 非接触形渦巻ばね

a. 巻数が多く外端固定支持の場合

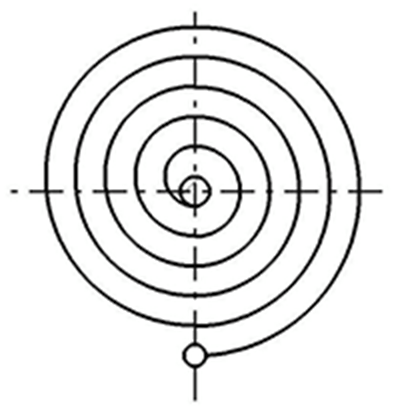
図1に、外端を固定支持、内端を巻心に取り付けた、巻数の多い非接触形渦巻ばねを示す。このときの設計式は次のとおりである。

（1）
（2）
（3）

b. 巻数が多く、外端ピン支持の場合

外端をピンジョイント等でピン支持とした場合の設計式は次のとおりである。

（4）
（5）
（6）

ピン支持された外端にモーメントが働かないため、外端を固定支持した場合と比べるとたわみ角が約25%増大する。また、曲げ応力はばね全体で変化し、最大曲げ応力の位置は外端近傍に位置する。同一トルクを与えた場合、曲げ応力は外端を固定支持した場合の2倍となる。

ii. ひげぜんまい

ひげぜんまいは、小型で巻数の多い非接触形ばねの一種だが、等時性という特性を有する。ひげぜんまいは、回転振動の中心とひげぜんまいの重心との偏心を小さくする設計が必要である。ひげぜんまいの設計方法の詳細はここでは省略する。
振動体の質量を Mv その回転半径をXとすれば、振動体の周期 Tは次のとおりである。

（7）

2接触形渦巻ばね
（ぜんまい）

i. S字ぜんまい

一次巻き加工を行い、その自由形状がS字に似た形状になる渦巻ばねを、S字ぜんまいと称する。

a. 回転数とばねの長さ

ばねの矢状面積（板厚×長さ）がケース内部の断面積から軸心の断面積を差し引いた有効面積の1/2を占めるように設定した場合、総回転数が最大値となる。このとき、トルクを加えていなければぜんまいがケースに密着する。また内端と軸心の密着巻部分を無視すれば、このときの総回転数Nは次のようになる。

（8）

ただし実際には、必要な回転数を確保するための長さに設定することが多い。

b. ぜんまいのトルク特性と応力

Ｓ字ぜんまいは、板の外側に初期応力として圧縮応力を与えてある。トルクMと応力σの関係は、

（9）

となる。この場合の応力σは、初期圧縮応力とばねの変形によって生じる引張応力の和となる。ばね有効長すべてに均等に負荷がかかっている状態の線形特性であるばね定数kは、

（10）

となる。これらの計算式では、ぜんまいの特性の一部しか表せないため、実際の計算は数値解析を行う必要がある。

ii. 一次巻なしぜんまい

直線形状の鋼帯を巻込んで作成されるぜんまいの設計式はS字ぜんまいと同様である。

iii. 定トルクばね

定トルクばねは、トルクを加えていないときの自然半径R_nに沿って密着巻したばねを、R_nより少し大きい半径の従動軸に取り付け、その自由端を駆動軸に取り付けたものである。これは、駆動軸を従動軸と同方向または反転方向に回転させることで動作する。定トルクばねは、回転数によらずトルクがほぼ一定という特徴をもつ。またR_nを変動させることで、トルクを一定ではなく、途中で変化させることもできる。さらに、回転数を確保しやすいという特徴ももっている。
ただし、応力振幅が大きくなるため、一般的に耐久性能は低くなる。

a. A-motor

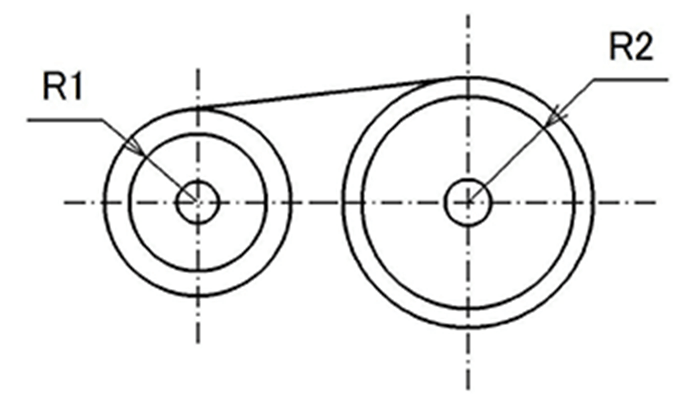
駆動軸と従動軸が同方向に回転する定トルクばねをA-motorと称する。
この場合のトルクMは、

（11）

b. B-motor

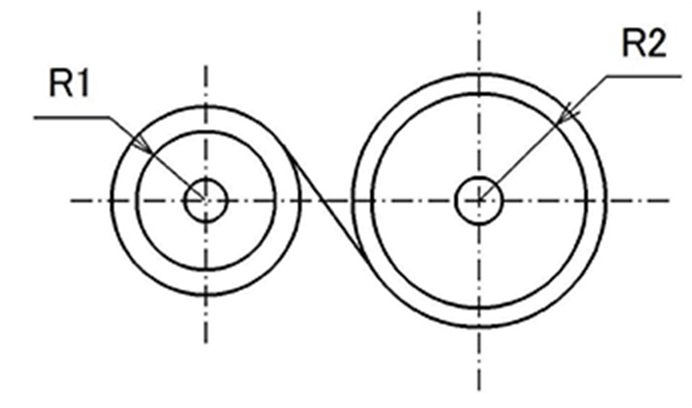
駆動軸と従動軸が同方向に回転する定トルクばねをB-motorと称する。
この場合のトルクMは、

（12）

iv. 定荷重ばね

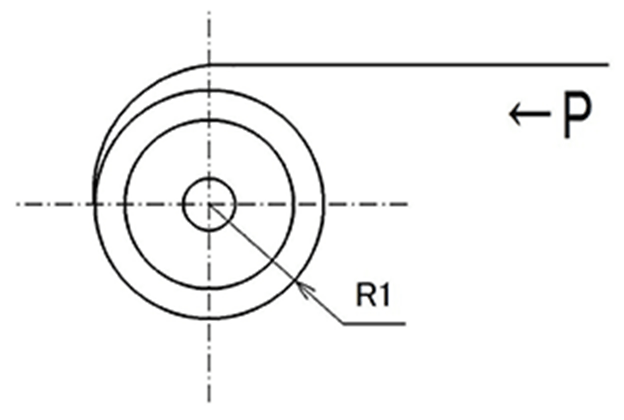
定トルクばねと同様に、外端を直線的に引き出して、その巻込む力を利用するものを定荷重ばねと称する。
この場合の荷重Pは、引き出し量とほとんど無関係にほぼ一定となる。

（13）

3設計応力の取り方

ぜんまいの場合、使用時の最大応力は材料の降伏点付近となるが、耐久性能を論じるときは応力振幅（応力範囲）の設計方法に焦点が当てられる。式（9）より、最大トルクと最小トルクの差から、応力振幅をある程度推察できる。しかし、実際には使用範囲内でケースまたはシャフトに密着している部分があり、その部位の応力振幅は小さくなり、それ以外の部分の応力振幅が大きくなる。そのため、数値解析により応力振幅を計算する必要がある。

4設計上の注意

一次巻を行わないぜんまいを設計する場合、直線の鋼帯から巻取られたばねはほとんどの領域で塑性変形し、トルクが負荷していない状態ではらせん形状となる。しかし、ばねの長さが長くなると、一部の領域で塑性変形が生じず、直線形状が残ることがある。この部位は、同時に同じような変形を起こすため、板間摩擦が大きくなり、ぜんまいの正常な動作を阻害する。これにより、みかけのトルクが低くなったり、耐久性が極端に悪化したりするので注意が必要である。

5設計例

前述したように、計算式だけで接触形渦巻ばねの設計をしようとすると、その概略を示すことしかできない。

i. ぜんまいの設計例

使用範囲が10回転、最低トルクMが100[N∙mm]としたぜんまいを設計する。使用する材質はSUS301とし、ケースの内径D₂を50[mm]、シャフト径d₁を10[mm]，板幅bを8[mm]とする。
まず、ぜんまいの最大トルクM_maxを150[N∙mm]と仮定する．S字ぜんまいとすれば、最大公称応力σ_maxは2400[MPa]程度となる（一次巻なしの場合σ_max=1800[MPa]程度）。式（9）より，板厚tは0.220[mm]とする。

また、総回転数を22回と仮定すると、このときの最大トルクは、M_max=155[N∙mm]である。
内端の焼鈍部分を1.5巻、すなわち50[mm]設けると仮定すると、シャフトに密着巻とすることができる。このときシャフト径は以下のようになる。

また、式（8）より、総回転数Nは、

ばねの長さは、

となる。トルクが負荷していないときにぜんまいはケースに密着していると仮定する。このときの総回転数は、シャフトに密着巻されているときの巻数と、ケースに密着しているときの巻数の差である。

総回転数が22回とすると、l=2160[mm]となる。
ヤング率Eを190[GPa]とすると、ばね定数は式（10）より、

使用範囲をN=8～18とすれば、

となる。このときの応力範囲∆σは、

となる。※

※ぜんまいのように、長方形断面の材料で幅が厚さに比べて大きい場合には、EIの代わりにEI⁄（（1-v^2 ））としたほうが正確な結果が得られる。
※当社データによると、∆σ≒600[MPa] が、100,000回の使用に耐えうる耐久性能の目安となる。

ii. 定荷重ばねの設計例

引き込み荷重P=10[N]の定荷重ばねを設計する。定荷重ばねは、R_nにコイリングされた薄板を直線に引き伸ばして使用する．薄板はいくら小さくコイリングしても直線に引き伸ばすと塑性変形を起こす。したがって、R_nの設定には制限がある。使用する材料にもよるが、板厚の40倍が最小R_nの目安となる。
さて、式（13）において、板厚t=0.200[mm]とすると製造可能な R_nはR_n≧8となる。いま R_n=10として、ヤング率190 [GPa]、従動軸半径10 [mm]とすれば、板幅bは、